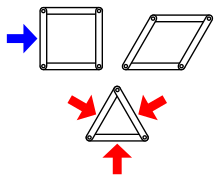
Structural rigidity is a combinatorial theory that predicts how flexible structures behave when rigid bodies connect through hinges or linkages.
Core Concepts
Rigidity Defines Structure’s Resistance
A structure’s rigidity determines its ability to maintain shape under force. When a structure won’t bend or flex under applied force, it’s rigid. The opposite state is flexibility. In practice, structures combine rigid components like straight rods with flexible connection points called hinges.
Two Types of Rigidity Shape Design
Finite rigidity (also called macroscopic rigidity) means a structure won’t flex, fold, or bend by any measurable amount. Infinitesimal rigidity prevents flexing at even theoretical microscopic levels. While finite rigidity’s benefits are clear, infinitesimal rigidity matters because tiny theoretical flexes can lead to real structural wear.
Mathematical Framework
Rigid Graphs Model Stability
A rigid graph exists in Euclidean space and won’t flex when its edges become rigid rods and vertices become hinges. Flexible graphs, in contrast, allow continuous vertex movement while maintaining distances between adjacent points.
Compression and Tension Elements
Structures can include compression elements that stretch but won’t shrink, and tension elements that shrink but won’t stretch. When combined in a rigid graph, these elements create a tensegrity structure.
Key Mathematical Findings
The field has produced several breakthrough discoveries. Cauchy’s theorem proves that three-dimensional convex polyhedra with rigid plate faces and hinged edges create rigid structures. The bellows conjecture, now proven, shows that flexible polyhedra maintain constant volume during motion.
Historical Development
James Clerk Maxwell, the renowned physicist, pioneered structural rigidity’s mathematical theory. The field saw significant growth in the late twentieth century and continues to evolve. Maxwell developed equations showing that in three dimensions, a structure’s force equilibrium depends on the relationship between connection points and connecting pieces.
Citations:
https://en.wikipedia.org/wiki/Structural_rigidity
In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.